 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设S1(t)是曲线=x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线=x与直线x=1及y=t
设S1(t)是曲线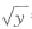 =x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线
=x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线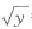 =x与直线x=1及y=t(0<1<1)所围图形的面积.试求生为何值时.S1(t)+S2(t)最小?最小值是多少?
=x与直线x=1及y=t(0<1<1)所围图形的面积.试求生为何值时.S1(t)+S2(t)最小?最小值是多少?
 答案
答案
 请输入或粘贴题目内容
搜题
请输入或粘贴题目内容
搜题
 拍照、语音搜题,请扫码下载APP
拍照、语音搜题,请扫码下载APP
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设S1(t)是曲线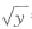 =x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线
=x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线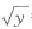 =x与直线x=1及y=t(0<1<1)所围图形的面积.试求生为何值时.S1(t)+S2(t)最小?最小值是多少?
=x与直线x=1及y=t(0<1<1)所围图形的面积.试求生为何值时.S1(t)+S2(t)最小?最小值是多少?
 答案
答案
 更多“设S1(t)是曲线=x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线=x与直线x=1及y=t”相关的问题
更多“设S1(t)是曲线=x与直线x=0及y=t(0<t<1)所围的图形的面积,s2(t)是曲线=x与直线x=1及y=t”相关的问题
第3题
第4题
A.高阶无穷小
B.低阶无穷小
C.同阶但非等价的无穷小
D.等价无穷小
第5题
设函数y=f(x)在(1,+∞)上连续,若曲线y=f(x),直线x=1,x=(>1)与x轴所围成的图形绕x轴旋转一周而成的旋转体体积为
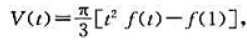
又知道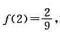 求f(x)。
求f(x)。
第6题
如图示,C1和C2分别是
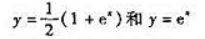
的图像,过点(0,1)的曲线C3是一单调增丽数的图像,过C2上任一点M(x,y),分别作垂直于Ox轴和Oy轴的直线lx和ly把C1,C2和lx所围成图形的面积记为S1(x);把C2,C3和ly所围成图形的面积记为S2(y).如果总有S1(x)=S2(y),求曲线C3的方程x=φ(y).
第7题
设X与Y是两个相互独立的随机变量,X在[0,1]上服从均匀分布,Y的概率密度为
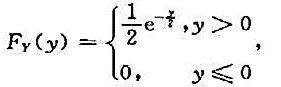
(1)求(X,Y)的联合概率密度;
(2)设关于t的二次方程为t2+2Xt+Y=0,求t有实根的概率。
第8题
设平面薄片所占的闭区域D由螺线p=2θ上一段弧(0≤θ≤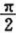 )与直线
)与直线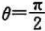 所围成,它的面密度为u(x,y)=x2+y2.求这薄片的质量.
所围成,它的面密度为u(x,y)=x2+y2.求这薄片的质量.
第9题
设f(x)∈C[a,b],在(a,b)内可导,且曲线y=f(x)非直线,证明:存在ξ∈(a,b),使得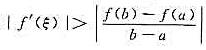 。
。